文章标题：The Staircase Mechanism in Differential Privacy
作者：Quan Geng, Peter Kairouz, Sewoong Oh, Pramod Viswanath
文章地址：https://ieeexplore.ieee.org/document/7093132
发表年份：2015

Abstract

通常来说我们在实现差分隐私（Differential Privacy, DP）的时候都是采用的 Laplacian 机制。但是却没人说明采用 Laplace 机制好不好，本文提出了一个叫做 Staircase Mechanism 的机制。提出的 Staircase 机制可以直接替代 Laplacian 机制。

Introduction

DP是一种隐私框架可以用来保护数据隐私。自从提出以来，DP被广泛用于各个方面。DP可以权衡数据有效性和隐私保护性（data utility and privacy）。最基本的情况可以认为是这样的：考虑一个数据查询者，他想要得到关于这个数据集的聚合信息。如果没有隐私需求的话，直接对这个数据集进行查询就可以了。为了保护隐私，需要对查询的结果进行一定处理，通常是加上一定的噪声。保护隐私的前提下，加的噪声需要满足这样的特性：数据集中任意一条记录的不同不会导致输出结果变化很大。这样即对数据集进行了查询又保护了每条记录的隐私。

形式化上，对数据集的查询可以认为是这样一个实值查询：

$q : \mathcal{D} \rightarrow \mathbb{R}^{d}$

其中，$\mathcal{D}$ 表示可能的数据集。

为了达成保护隐私情况下进行查询，我们需要额外引入一些知识，首先是差分隐私：

机制 $\mathcal{K}$ 是 $\epsilon$-DP 的，如果对于任意相邻数据集 $D_1, D_2$ 以及查询的任意输出 $S \subset \operatorname{Range}(\mathcal{K})$ 有：
$\operatorname{Pr}\left[\mathcal{K}\left(D_{1}\right) \in S\right] \leq \exp (\epsilon) \operatorname{Pr}\left[\mathcal{K}\left(D_{2}\right) \in S\right]$

一组查询可以实际上写成这样的形式：$q(D)=\left(q_{1}(D), q_{2}(D), \ldots, q_{d}(D)\right)$

为了了解查询的性质，我们还需要了解查询的敏感度，敏感度的定义如下：

对于查询 $q : \mathcal{D} \rightarrow \mathbb{R}^{d}$，其敏感度定义为：
$\Delta :=\max _{D_{1}, D_{2} \in \mathcal{D}}\left\|q\left(D_{1}\right)-q\left(D_{2}\right)\right\|_{1}$

通常来说，最标准的满足DP的方法是再买个查询后面加上一定的噪声，即机制 $\mathcal{K}$ 为：

$\mathcal{K}(D)=q(D)+X=\left(q_{1}(D)+X_{1}, \dots, q_{d}(D)+X_{d}\right)$

其中，每一个查询后面的 X 表示加如的噪声，通常来说，我们采用拉普拉斯机制作为噪声。结合查询的敏感度，机制 $\mathcal{K}$ 可以写成如下形式：

$\begin{aligned} \mathcal{K}(D) & :=q(D)+\operatorname{Lap}\left(\frac{\Delta}{\epsilon}\right)^{d} \\ &=\left(q_{1}(D)+\operatorname{Lap}\left(\frac{\Delta}{\epsilon}\right), \ldots, q_{d}(D)+\operatorname{Lap}\left(\frac{\Delta}{\epsilon}\right)\right) \end{aligned}$

以上的拉普拉斯机制目前被作为DP的最基本方法广为使用。然而并没有对 Laplace 进行优化的相关工作。本文中，我们提出了一种可以替代 Laplace 的方法，满足同样的 DP 保护程度下，我们的方法所添加的噪声更小。

Staircase Mechanism

我们定义了一个多维对称分布的概率分布，其图像呈阶梯状，因此称为 Staircase 机制。给定 $\gamma \in[0,1]$，我们定义 $\mathcal{P}_ {\gamma}$ 为概率分布，其概率密度函数为 $f_{\gamma}(\cdot)$：

$f_{\gamma}(\mathbf{x})=\left\{\begin{array}{ll}{e^{-k \epsilon} a(\gamma)} & {\|\mathbf{x}\|_{1} \in[k \Delta,(k+\gamma) \Delta)} \\ {e^{-(k+1) \epsilon} a(\gamma)} & {\|\mathbf{x}\|_{1} \in[(k+\gamma) \Delta,(k+1) \Delta)}\end{array}\right.$

当然，为了满足归一化的需求，需要积分等于1，然后这个参数 $a(\gamma)$ 就可以求出来等于：

$a(\gamma) \triangleq \frac{d !}{2^{d} \Delta^{d} \sum_{k=1}^{d}\left(\begin{array}{l}{d} \\ {k}\end{array}\right) c_{d-k}\left(b+(1-b) \gamma^{k}\right)}, c_{k} \triangleq \sum_{i=0}^{+\infty} i^{k} b^{i}$

根据这个公式的性质，很显然有：

$f_{\gamma}(\mathbf{x}) \leq e^{\epsilon} f_{\gamma}(\mathbf{x}+\mathbf{t}), \forall \mathbf{x} \in \mathbb{R}^{d}, \forall \mathbf{t} \in \mathbb{R}^{d} \text { s.t. }\|\mathbf{t}\|_{1} \leq \Delta$

也就是说，这个 Staircase 机制是满足 $\epsilon$-DP的。

那么这个概率分布到底长啥样呢，下面的图1和图2就展示了一维和二维情况啊下的一个概率密度函数。

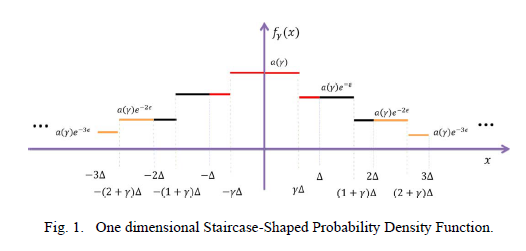
fig01

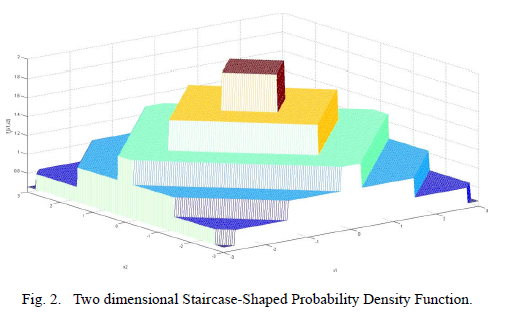
fig02

有了这个概率密度函数之后，究竟如何根据这个概率密度函数生成一个随机噪声呢？作者给出了算法1，如下：

alg01

其中，S决定了这个噪声的符号，G决定了噪声在区间 $[G \Delta,(G+1) \Delta)$ 中，B决定了噪声在区间的前半部分 $[G \Delta,(G+\gamma) \Delta)$ 还是后半部分 $[(G+\gamma) \Delta,(G+1) \Delta)$，然后 U 是用来在区间随机化采样。根据这个过程，我们就产生了一个 Staircase 的噪声分布了。

Comparison with Prior Work

在目前现有的工作中，一般采用方差或者噪声的期望来衡量 DP 在数据有效性和隐私性的权衡。我们在之前的文章 [3] 中证明了在最小化代价函数的前提下：

为每个查询添加独立的噪声是最优的
Laplacian 分布并不是最优的噪声添加函数，最优的噪声添加函数应该是类似阶梯状的。

Optimality of Staircase Mechanism

前面说了，满足隐私保护的查询机制可以表示为：$\mathcal{K}(D)=q(D)+X=\left(q_{1}(D)+X_{1}, \ldots, q_{d}(D)+X_{d}\right)$，其中 X 表示加在查询结果上的噪声，那么在 DP 的要求下，有：

$\begin{aligned} \operatorname{Pr}\left[\mathcal{K}\left(D_{1}\right) \in S\right] & \leq e^{\epsilon} \operatorname{Pr}\left[\mathcal{K}\left(D_{2}\right) \in S\right] \\ \Leftrightarrow \operatorname{Pr}\left[q\left(D_{1}\right)+X \in S\right] & \leq e^{\epsilon} \operatorname{Pr}\left[q\left(D_{2}\right)+X \in S\right] \\ \Leftrightarrow \operatorname{Pr}\left[X \in S-q\left(D_{1}\right)\right] & \leq e^{\epsilon} \operatorname{Pr}\left[X \in S-q\left(D_{2}\right)\right] \\ \Leftrightarrow \operatorname{Pr}\left[X \in S^{\prime}\right] & \leq e^{\epsilon} \operatorname{Pr}\left[X \in S^{\prime}+q\left(D_{1}\right)-q\left(D_{2}\right)\right] \end{aligned}$

其中，$S^{\prime} \triangleq S-q\left(D_{1}\right)=\left\{s-q\left(D_{1}\right) | s \in S\right\}$。因为我们有 $\left|q\left(D_{1}\right)-q\left(D_{2}\right)\right|_{1} \leq \Delta$，所以，根据上式，有：

$\operatorname{Pr}\left[X \in S^{\prime}\right] \leq e^{\epsilon} \operatorname{Pr}\left[X \in S^{\prime}+\mathbf{t}\right]$

根据给定的概率密度函数，我们有：

$e^{-\epsilon} \leq \frac{f_{X}(\mathbf{u})}{f_{X}(\mathbf{u}+\mathbf{t})} \leq e^{\epsilon}, \quad \forall \mathbf{u} \in \mathbb{R}^{d}, \mathbf{t} \in \mathbb{R}^{d}$

为了衡量方法的有效性，我们定义了一个 cost 函数，为：$\mathcal{L}(\cdot) : \mathbb{R}^{d} \rightarrow \mathbb{R}$。那么这个 DP 的优化问题就等价于下式：

$\begin{array}{c}{\underset{\mathcal{P}}{\operatorname{minimize}} \iint \cdots \int_{\mathbb{R}^{d}} \mathcal{L}\left(x_{1}, x_{2}, \ldots, x_{d}\right) \mathcal{P}\left(d x_{1} d x_{2} \ldots d x_{d}\right)} \\ {\text { subject to } \mathcal{P}(S) \leq e^{\epsilon} \mathcal{P}(S+\mathbf{t})} \\ {\quad \quad \forall \text { measurable set } S \subseteq \mathbb{R}^{d}, \forall\|\mathbf{t}\|_{1} \leq \Delta}\end{array}$

其中 $\mathcal{P}(S)$ 表示概率 $\operatorname{Pr}[X \in S]$，上式的意思就是在满足 DP 的前提下最小化给定的代价函数。所以这里当然有一个问题就是代价函数是啥。当然，不同的应用环境可能有不同的代价指标。作者给出了这样一个代价函数：

$\mathcal{L}\left(x_{1}, x_{2}, \ldots, x_{d}\right)=\sum_{i=1}^{d}\left|x_{i}\right|, \quad \forall\left(x_{1}, x_{2}, \ldots, x_{d}\right) \in \mathbb{R}^{d}$

再假定 $\mathcal{S P}$ 是所有满足条件的概率分布，那么本文的主要贡献就是证明了对于这个 L1 代价函数，我们的 Staircase 机制是最优的。即定理1：

对于 $d=2$ 以及 $\mathcal{L}(\mathbf{x})=|\mathbf{x}|_{1}, \quad \forall \mathbf{x} \in \mathbb{R}^{2}$，那么：
$\begin{aligned} & \inf _{\mathcal{P} \in \mathcal{S} P} \iint_{\mathbb{R}^{2}} \mathcal{L}(\mathbf{x}) \mathcal{P}\left(d x_{1} d x_{2}\right) \\=& \inf _{\gamma \in[0,1]} \iint_{\mathbb{R}^{2}} \mathcal{L}(\mathbf{x}) f_{\gamma}(\mathbf{x}) d x_{1} d x_{2} \end{aligned}$

这个证明的过程就不仔细展开了，我也没有逐一推敲，感兴趣的读者可以参考原文。上述定理只针对了二维的情况，同样作者给出了定理2，说的是对于 $d > 2$，Staircase 依然是最优的。

Implications

我们已经知道 Staircase 是最优的了，那么 Staircase 里面有三个参数：$\epsilon, \delta$ 和 $\gamma$。其中 $\epsilon, \delta$ 我们是 DP 要求和查询函数的固有性质，不可更改。那么 $\gamma$ 该怎么取呢？作者沿用了之前自己的论文，说 $d=1$ 的时候该这么取：

$\gamma^{*}=\frac{1}{1+e^{\epsilon / 2}}$

对应的噪声的 amplitude （这个东西可以理解为平均的误差吧）是：

$V_{1}^{*}=\Delta \frac{e^{\epsilon / 2}}{e^{\epsilon}-1}$

与之对应，如果采用 Laplace 的化，其 amplitude 为：

$V_{L a p} \triangleq \int_{-\infty}^{+\infty}|x| f(x) d x=\frac{\Delta}{\epsilon}$

然后作者比较 $V\left(\mathcal{P}_{\gamma^{*}}\right)$（这篇文章目前没有看到这个东西咋算出来的），说很显然当 $\epsilon$ 很小的时候，Laplace 是 asymptotically optimal 的。二者的差是：

$V_{L a p}-V\left(\mathcal{P}_{\gamma^{*}}\right)=\Delta\left(\frac{\epsilon}{24}-\frac{7 \epsilon^{3}}{5760}+O\left(\epsilon^{5}\right)\right)$

当 $\epsilon$ 较大的时候，有：

$\begin{aligned} V_{L a p} &=\frac{\Delta}{\epsilon} \\ V\left(\mathcal{P}_{\gamma^{*}}\right) &=\Theta\left(\Delta e^{-\epsilon / 2}\right) \end{aligned}$

这一章节是对 Staircase 机制的一些分析，由于我没有参考给出的引用论文，这里暂且只给出了作者文中的结论了。作者还给出了一些分析，就不细说。